Full Extents Pan Zoom In Zoom Out Identify Print Map Search Tools Measure Tools Zoom to Item Print Item Link to Report Page Link to Property Record Card Link to Deed.

The Trader's Cheat Sheet is a list of 44 commonly used technical indicators with the price projection for the next trading day that will cause each of the signals to be triggered. The Trader's Cheat Sheet is updated for the next market session upon receiving a settlement or end. Coq Cheatsheet When proving theorems in Coq, knowing what tactics you have at your disposal is vital. In fact, sometimes it’s impossible to complete a proof if you don’t know the right tactic to use! We provide this tactics cheatsheet as a reference. Coq Cheatsheet for Emacs! This is really just something for myself, but by all means, if you can use it go ahead! – and don’t be selfish about leaving your favourite shortcut in the comments!

Table of Contents

• 2. Automation facilities
  • 2.1. Using tactics like reflexivity over user built relations
  • 2.2. Using hint databases
  • 2.3. Computation
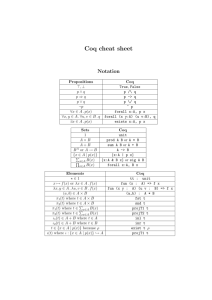
• 3. Notations
• 4. Working with Ltac
  • 4.1. Matching on hypotheses and conclusions
• 5. Miscellaneous useful tricks
  • 5.2. Duplicating an hypothesis
• 6. Arguments
• 8. Intro patterns
• 9. Pattern matching. Unify with intro patterns and talk about the let, let with the backstick
• 10. Switching and selecting goals
  • 10.2. Goal selectors.
• 11. Emacs extensions: Proof-General and Company-coq

1 Useful user-defined tactics** The Case tactic

Taken from Pierce's Software Foundation, it can be used to document a proof by annotating the proof context with the ongoing case.

I often need to perform case analysis on the discriminee of a matchconstruct. To do so, use the following tactic:

From this you can build your own variant of the tactic that runs arbitrarytactics after destructing, for instance simplifying or trying to eliminate simplgoals. My variant simplifies in the whole context and tries to solve goals usingintuition congruence.

2 Automation facilities

2.1 Using tactics like reflexivity over user built relations

The goal here is to be able to use coq's built-in tactics over other relationsthan iff and eq, in particular relations that you have defined yourself.

2.1.1 Adding equivalence relations, preorder, etc…

The inner mechanism going on when using tactics like reflexivity,transitivity or symmetry is typeclasses. However coq allows a particularfacility to declare new relation without digging into this. The syntax goesroughly as follows:

Note that you naturally only want to take A as a parameter if your relationis indeed polymorphic. For instance, suppose you need to manipulatepredicates over program states up to propositional extentionalequivalence. This relation is an equivalence relation, so you might want todeclare it as so.

We now are able to prove goals such that (forall P: Pred, PEq P P) with asimpl (intros P; reflexivity). Same goes for transitivity and symmetry.

Note that we can also only declare some of those properties, declaring that arelation is a preorder for instance:

In this case naturally symmetry will not work. Note that you are notrequired to provide the appropriate proof term directly in the relationdeclaration, you may use wildcards for coq to require the proofsinteractively.

Remark: As said earlier, what is really going on is the typeclassmechanism. So all this is simply sugar for an instance declaration to theappropriate type class, Equivalence for example in the first case. We couldhave written instead:

2.1.2 Adding morphisms

The other typical case in which you might want to extend built-in tactics isthe one of morphisms for which we would like to be able to userewrite. Once again, we have syntactic sugar to avoir bothering explicitelywith typeclasses. In the case of a binary function, it would look like this:

This one might seem a bit more cryptic. What is going on is that given acontext, we want to be able to substitute a subterm for an other one giventhey are related by the relation rel. Said differently, we want to prove thatf is a morphism with respect to rel, or that rel is compatible with f.

It is clearer with an example. Say we define the union of two predicates, wecan actually rewrite any equivalent predicates under it.

coq asked us to prove that if four predicates are pairwise PEquivalent, theirrespective unions are PEquivalent. We therefore now are able to use thetactic rewrite to rewrite PEquivalences under unions in goals.

Note: beware, we only proved the compatibility of PEq with respect to theunion! coq will complain if we try to rewrite PEquivalence under any otherconstruction. The (Leibniz) equality has the peculiar property to becompatible with any context by definition.

Note bis: we have a very symmetric statement in the exemple using PEqeverywhere, but that is not necessary. We could for instance assertcompatibility only on the left by replacing the second PEq by an eq. An otherreason of uniformity in the example is that the codomain of the functionPJoin is the same as its arguments, but once again it could be otherwise. Itnotably is common to end up in Prop and therefore be interested in a resultwhere the last PEq is replaced by iff: the proposition obtained afterrewriting is guaranteed to be equivalent.

Finally, as was the case with relations, we can instead explicitely declarethe adequate instance. The Typeclass at use here is Proper:

2.2 Using hint databases

2.2.1 Hint databases from the standard library

How To Use Coq

The auto (or its existential variant) tactics tries by default to solve a goal byexploring proofs trees, up to a fixed depth, that could be built usinga fixed set of rules.These rules are defined in a so-called database, named core,essentially trying to unfold a few arithmetic and boolean functionsfrom the standard library, and trying to apply a few lemmas andconstructor over the elementary logical connectives. Its detail can beprinted through the command:

However, the auto tactics can be prompted to use another hintdatabase. Are predefined the following, whose detail can be printed asseen previously: arith, zarith, bool, datatypes, sets andtypeclass_instances. Note that the last one is automatically enriched whenregistering new instances for a typeclass, and used during resolution.The syntax to use a specific database is the following:

2.2.2 User-defined databases

One can also define its own databases, for instance to reduce a userdefined expression to its normal-form via rewriting lemmas. Its creation is done through the Create HintDb command:

The user can then enrich the database by adding hints to it. A hint isa lemma (actually more generally a term) and a way to use it:

• by applying it (adds 'simple apply term' to the db): keyword Resolve
• by succeeding applying it (adds 'simple apply term; trivial' to thedb): keyword Immediate
• by adding constructors of a type as Resolve hints: keywordConstructors
• by allowing auto to unfold a definition: keyword Unfold
• by applying any tactic: keyword Extern.

For instance:

For more details: https://coq.inria.fr/refman/Reference-Manual010.html#sec395

2.3 Computation

2.3.5 NoteReflexivity

Reflexivity does more than simpl, it notably tries to unfold definitions.

3 Notations

3.1 Useful notations from the standard library

Importing the utf8 standard library defines a few convenient utf8-based notations. In particular an elegant way to define anonymous functions:

3.2 Precedence levels

Go from 0 (tightest) to 100, with an additionnal special 200.

3.3 Associativity

No associativityLeft associativityRight associativity

4 Working with Ltac

4.1 Matching on hypotheses and conclusions

4.1.1 Hypotheses

Looking for an hypothesis of the form P x y, for any x and y.

This will fail if no such hypothesis exists.You can add try in front of it.

To match all such hypotheses, add repeat.

The following example shows how to use hypotheses matching to remove duplicates in hypotheses.

We try to match two hypotheses of the form P ?x ?y. The pattern matching is strong enough to express that H1 and H2 must refer to the same x and y.H1 and H2 are guaranteed to be different though.

It is also possible to match part of an hypothesis.Using context:

4.1.2 Conclusions

The matching can also be made on the conlusion of the goal (after |-):

Of course, multiple patterns can be matched.

This will loop as long as either the hypotheses or the conclusion contain a term matching P ?x ?y.Be sure to remove the matching hypotheses to enforce termination.

4.2 Generate fresh names

Sometimes we need to generate fresh names inside tactics:

4.3 Print Ltac

One can view the Ltac code of a tactic (when it's actually written in Ltac).

4.4 Working with PG

One can add custom keybindings to Emacs / PG.For example, to see the Ltac code of a tactic (see previous section), we can define the following Emacs lisp code in the appropriate file (~/.emacs= in my case)

(PW: I should investigate what occurences of 'Print Ltac' stand for what)

5 Miscellaneous useful tricks

Coq Rewrite

5.1 Keeping track of the ongoing case

If proceeding by induction or case studies over an inductive case,say a semantic judgment, it can be hard to spot which case we endup in. A useful hack is to keep track of a discriminatingparameter. Assuming for example that we are about to inverse ajudgment such as (i, σ) → (i', σ'), simply use the followingtactics beforehand:

5.2 Duplicating an hypothesis

5.3 Show the axioms used for a given lemma

To show what axioms a given lemma depends on, one can use the following vernacular command

6 Arguments

6.1 Implicit arguments

Implicit arguments are treated the same way as if provided as an _, but systematically.We can declare them at define time by putting curly brackets around the argument.

Afterwards, through the Arguments directive: name and list of arguments, curlybrackets for the ones to be inferred.

Use an @ to disable implicit arguments locally.

Coq Tutorial

6.2 Arguments renaming

Arguments can be used to rename arguments using the rename flag (:rename. at the end of the command).(PW: explain? example?)

7 Generalize dependent versus generalize versus revert

Starting from a goal

One can use different tactics to move hypotheses from the context to the goal.

OR

Notice that the generalized hypothesis is still present in the context, contrary to the reverted one.

We can also generalize terms of type in Type.

Here we have lost some information, because the a in the context is no longer related to the new one.This situation is solved using generalize dependent.

8 Intro patterns

8.1 With square brackets

Conjunction: just a list with no separatorsEx: [H1 [H2 H3]] or (H1 & H2 & H3)Disjunction: |Ex: [H1 | H2]

Coq Cheat Sheet 2019

8.2 Tricks

<- or -> to rewrite directly an equality._ clear the hypothesis directly? to let coq choose the name

9 Pattern matching. Unify with intro patterns and talk about the let, let with the backstick

9.1 A particular case of pattern matching, the let-binding

Coq does not allow pattern matching over arguments of a function, as opposed to OCaml, even if the inductive type of this constructor admits a unique constructor. One can avoid an arguably heavy match using the let-binding construct:

Coq Tactics Cheat Sheet

Note however that by default, you can only destruct one layer of the argument. Using a tick allows you to destruct at arbitrary depth:

10 Switching and selecting goals

When several subgoals are left to solve, it is possible to solve some goalsbefore others (either because you don't feel in the mood for a given subgoal orbecause solving some goal will instantiate lots of existential variables, makingit easier to solve the remaining goals afterwards).

10.1 Switching to a specific goal

You can switch to solve goal num with the Focus vernacular command:

10.2 Goal selectors.

When the proof of the n-th goal is fairly easy, i.e. it is doable in a singletactic, we can use goal selectors that look more lightweight.

To apply tactic tac to the n-th subgoal:

10.2.1 In 8.5, the all: selector

In Coq 8.5, the all: selector applies a given tactic to all goals. This seemsvery handy in cases where a eapply has generated lots of existentials, most ofwhich would be solved in a particular subgoal. The strategy I would use here isto apply some tactic to the most discriminant subgoal and then call auto oreauto on the rest of the subgoals.

11 Emacs extensions: Proof-General and Company-coq

Coq Cheat Sheet Template

11.1 Proof-General

Proof-General is an Emacs interface for proof assistants such as Coq. The latest version is available on GitHub.

11.2 Company-coq

Company-coq is an extension for Proof-General's Coq mode. It is available through MELPA. One of its most interesting feature is prettification.For example, adding the following bits of code into your `~/.emacs` will visually replace all alpha with an α.

You will however need to use a font that can handle unicode. For example on OS X, you may need to add the following code into your `~/.emacs`: